Steer-by-wire kormányrendszer járműmodell alapú irányítása
Ideális kormányrendszerrel a jármű kanyarodását közvetlenül lehet meghatározni a kormánykerékkel a körülményektől függetlenül, miközben a jármű dinamikájáról és a környezetről is visszacsatolást kell biztosítani a vezető részére a kormányrendszeren keresztül. Ehhez ún. steer-by-wire technológia szükséges. Célunk egy ideális kormányrendszer szabályozó rendszerének kifejlesztése. Egyszerű, lineáris jármű és kormányzási modellt állítottunk fel, melyeket mérések alapján identifikáltunk. Az egyesített modellre különböző szabályozókat (PID, LQ, H∞) terveztünk, melyek performanciáit megvizsgáltuk nemlineáris veDYNA járműszimulációs rendszerben.
The ideal steering system directly determines the direction of the car independently from the effects of the environment while it provides a feedback to the driver. It requires the use of steer-by-wire technique. Our aim is to develop the control of the ideal steering system. Linear vehicle model and steering model are established and they are identified based on realistic vehicle simulation (veDYNA). These models are integrated. Different controllers (PID,LQ,H∞) are designed based on the integrated model. Their performances are analyzed in the vehicle simulator.
Bevezetés
Járműmodell
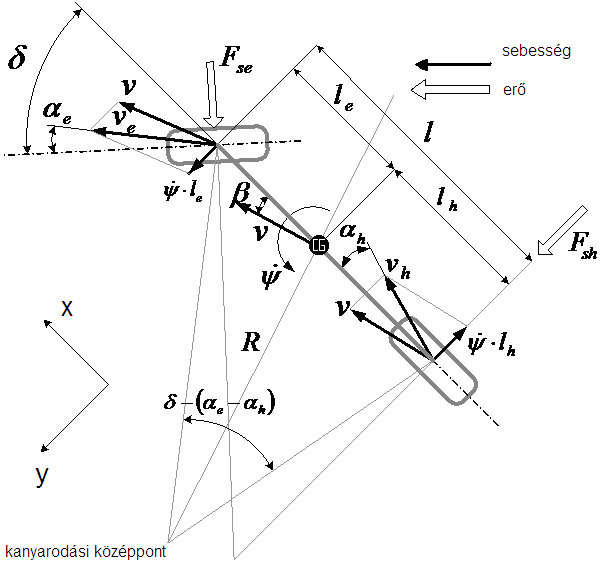
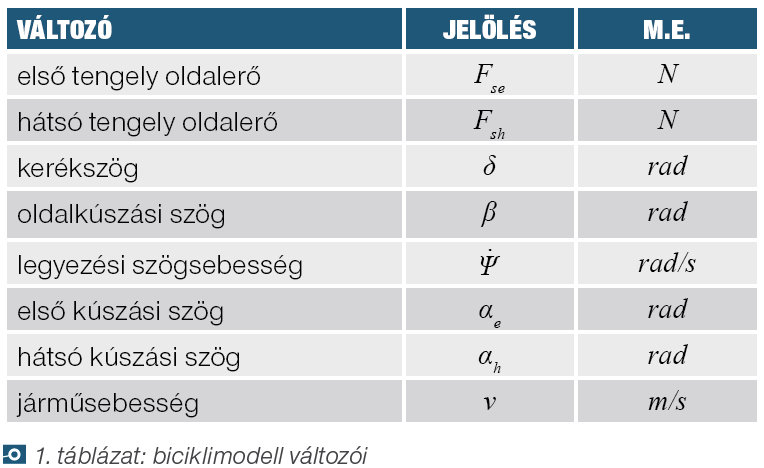
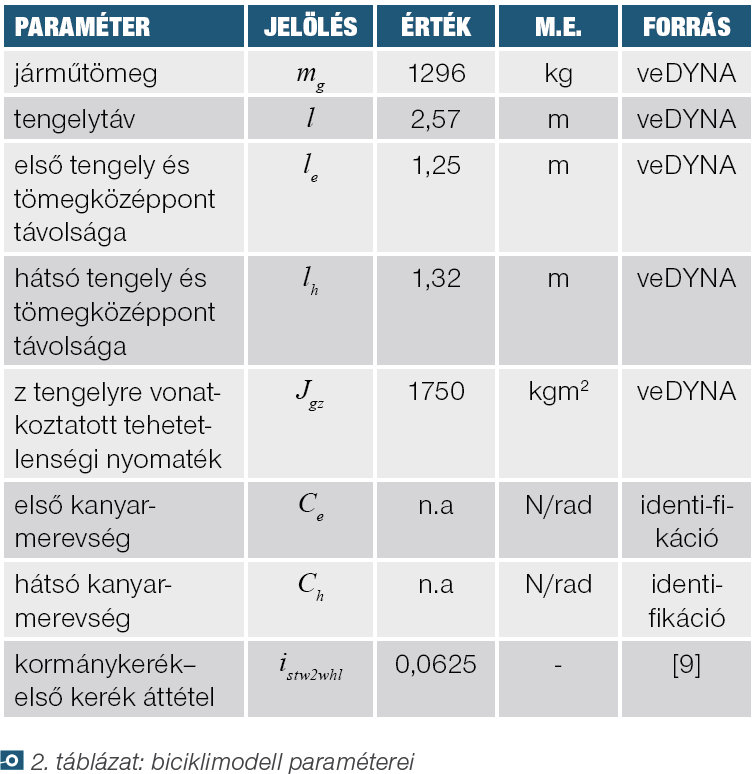
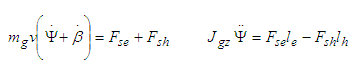
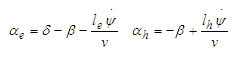
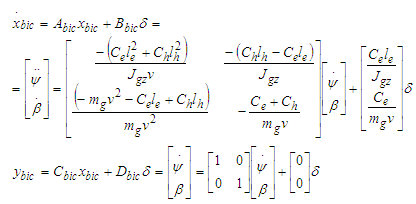
Járműmodell paraméter identifikáció
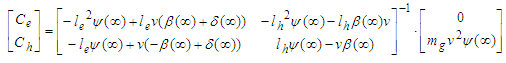
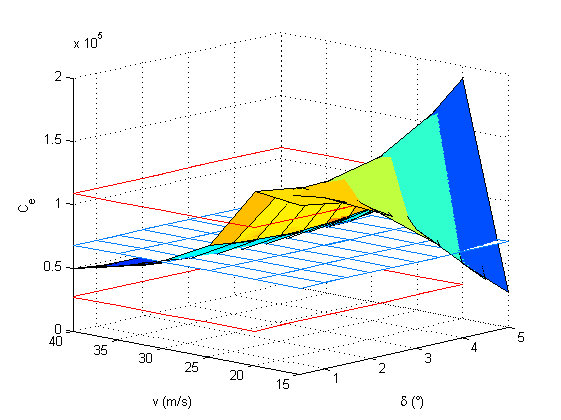
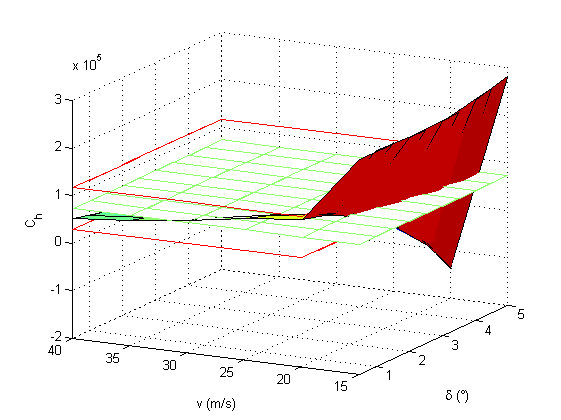
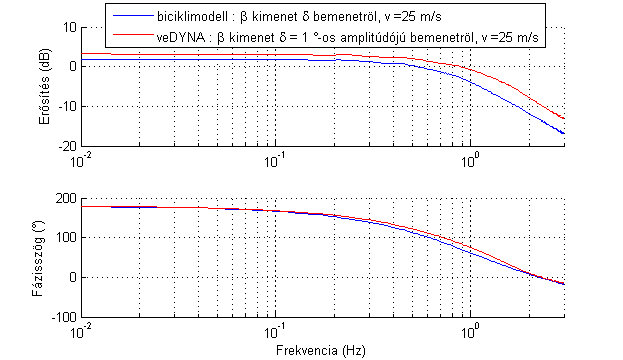
Dinamikus verifikáció
SBW alsó rendszer modell
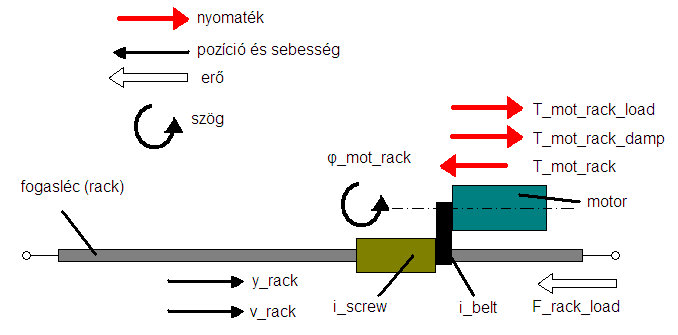
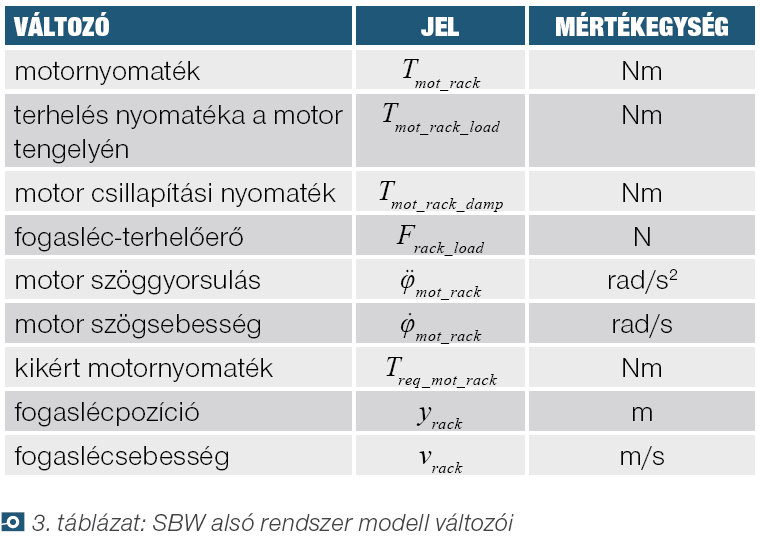
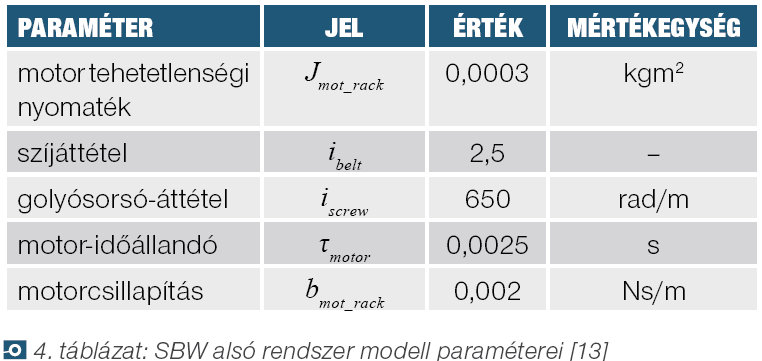
A 6. ábra alapján felírhatóak a (6) dinamikai egyenletek.
(6) 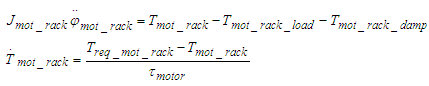
A dinamikai egyenletbe behelyettesítjük csillapítási- és terhelőnyomatékra felírt (7) egyenleteket.
(7) 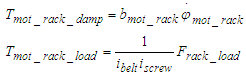
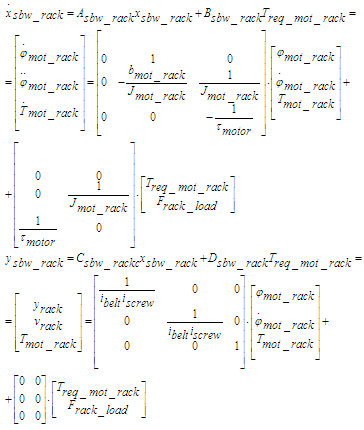
A (6) és (7) egyenletek alapján előállítható a (8) állapotegyenlet.
(8) 
Egyesített modell
Az egyesített modell célja a biciklimodell és a SBW modell összekapcsolása. Ehhez a bemenetek és a kimenetek közötti kapcsolatnak megfelelő definiálása szükséges, ahogyan az a 6. ábrán is látható. A biciklimodell kerékszöge és a fogasléc között kinematikai kapcsolat áll fenn, az áttételt [13] alapján irack2wheel = 6,25 rad/m értékűnek választjuk. A modellek közötti kapcsolatot a (9) egyenletek írják le.
(9) 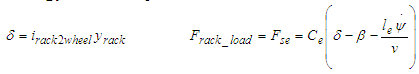
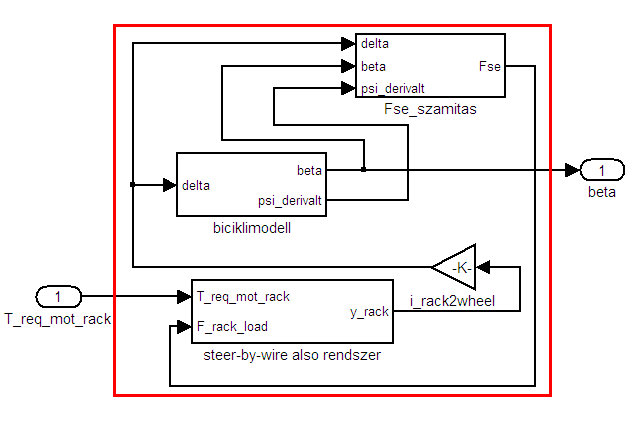
6.ábra: Egyesített modell
A (4),(8),(9) összefüggésekből felírható az egyesített modell (10) állapotegyenlete.
(10)

Szabályozás tervezése
A jármű irányításához szükséges szabályozó tervezését állandó sebességen (25 m/s) valósítjuk meg a lineáris egyesített modellen. Az egyesített modell szabályozott jellemzője a β oldalkúszási szög, a beavatkozó jel pedig a Treq_mot_rack kikért motornyomaték. A szabályozás célja a valóságot közelítőleg jól leíró nemlineáris veDYNA szimulátor járművének referenciakövetése minimális végérték hibával és túllövéssel, gyors dinamikával az értelmezési tartományban. A PID szabályozó a további szabályozókhoz viszonyítási alapot jelent adott munkapontban, az LQ szabályozótól a stabilitást és gyors performanciát várjuk el egy viszonylag széles tartományban, a H∞ szabályzótól pedig robosztusságot és megfelelő performanciát várunk el.
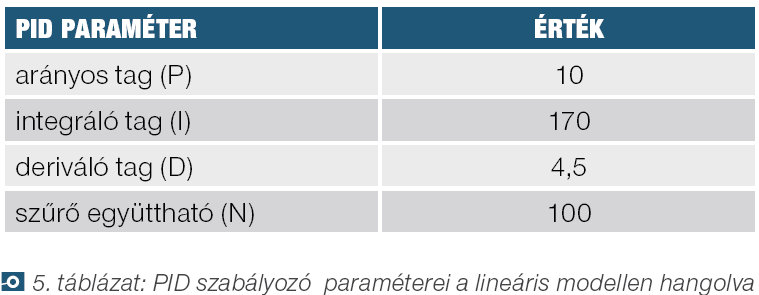
A PID szabályozó [2] tervezéshez a MATLABSimulink beépített PID blokkját használjuk, a paraméterek hangolása az 5. táblázatban összefoglalt eredményeket adta, a fázistartelék 75 fok.
Az LQ [3],[6] szabályozó tervezéséhez az egyesített modell kimenetének csak az oldalkúszási szöget hagyjuk meg, így SISO rendszert kapunk. A teljes állapotvisszacsatolással történő szabályozáshoz az egyesített modell állapotvektorának minden eleme előállítható a veDYNA-ból, illetve az alsó rendszer lineáris modelljéből, megfigyelő tervezése nem szükséges. A szabályozó tervezéshez a MATLAB lqry parancsát használjuk, hogy a beavatkozó és a kimeneti energiát közvetlenül súlyozhassuk. A kimeneti és a beavatkozó jel súlymátrixai a (11) egyenletekben láthatók.
(11) ![]()
A H∞ [4],[5],[6] szabályozó tervezésekor az LQ szabályozónál is felhasznált egyesített modell egybemenetű-egykimenetű változatára tervezzük a szabályozót. A tervezéshez MATLAB hinfsyn parancsát használjuk. A 7. ábrán látható a tervezéshez használt P-K struktúra.
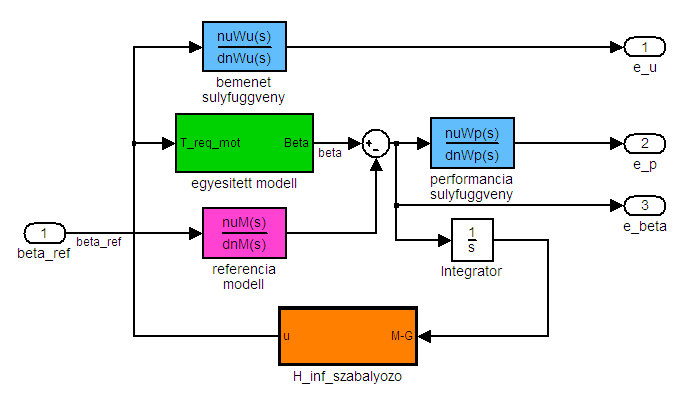
7.ábra: H∞ szabályozó P-K tervezési struktúra
A szabályozás tervezési paraméterei: a referencia modell (12) átviteli függvénye (mely egy kéttárolós lengőtag, a zérusokat a szabályozó-tervező algoritmus numerikus stabilitása érdekében vettük fel); a performancia és a beavatkozó jel súlyfüggvényei (13).
(12) 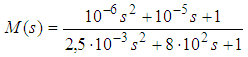
(13) 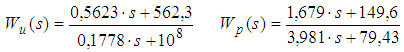
Szabályozás tesztelése
A lineáris modellen realizált szabályozásokat beépítettük veDYNA-ba és a lineáris modellen megtalált paramétereket kezdeti értékként használva finomhangoltuk. A PID szabályozó paramétereit nem volt szükséges módosítani, a fázistartalék 75 fok maradt. Az LQ szabályozó újrahangolt kimeneti súlymátrixa a (14) összefüggésben látható. A H∞ szabályozó újrahangolt bemeneti súlyfüggvényét pedig a (15) összefüggés adja meg.
(14) ![]()
(15) 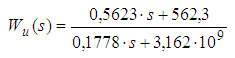
Az egyes szabályozók összehasonlítását számos sebesség és referenciaérték esetén elvégeztük. A 8. ábrán látható ezek közül egy esetben a szabályozott jel, továbbá a 9. ábrán ugyanezen esetben látható a beavatkozó jel alakulása a különböző szabályozók esetén.
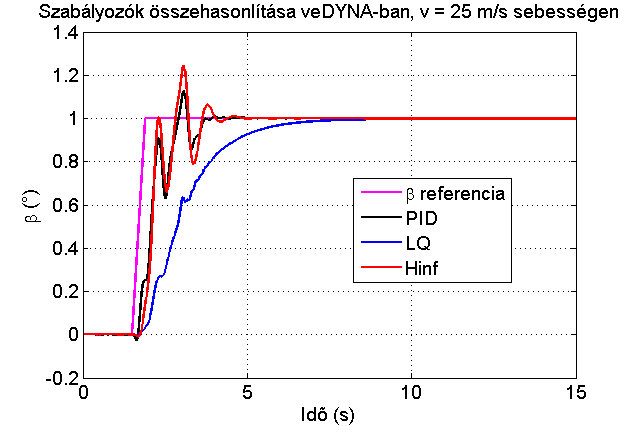
8.ábra: Szabályozók összehasonlítása veDYNA-ban 25 m/s sebességen 1 fokos oldalkúszási szög referencia mellett – referenciakövetés
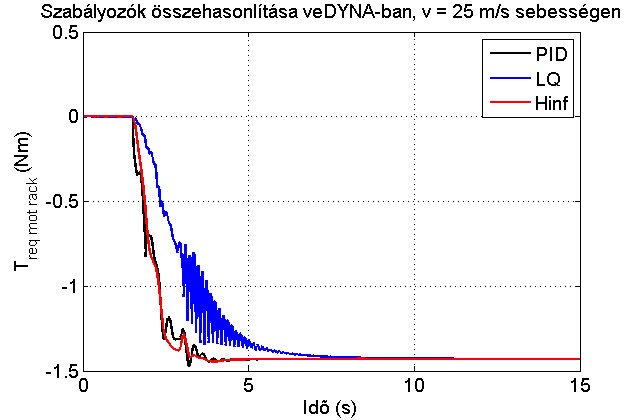
9.ábra: Szabályozók összehasonlítása veDYNA-ban 25 m/s sebességen 1 fokos oldalkúszási szög referencia mellett – beavatkozó jel
A 8. ábrán átható, hogy a munkapontban a PID és a H∞ szabályozó közel azonos gyorsasággal és túllendüléssel reagálnak. Az LQ lassabb dinamikával működik, mert a bemeneti súly további növelésével a beavatkozó jel erőteljesen oszcillálni kezd, ahogyan az már a 9. ábrán is kezd megmutatkozni. A H∞ szabályozó túllendülése további hangolásokkal csökkenthető, de robosztusságának köszönhetően már ilyen paraméterek mellett is alacsonyabb sebességeken (a biciklimodell értelmezési tartományán kívül) még megfelelő performanciával és stabilan működik, ellentétben a másik két szabályozóval.
Továbblépési lehetőségek a járműmodellben
A modellalapú tervezés tényleges előnyei egy pontosabb járműmodell esetén markánsabban érzékelhetők. A jelenleg használt lineáris modell egy igen szűk tartományban használható, a továbblépés mindenképpen nemlinearitások bevezetését jelenti. A járműmodell célszerű bővítési lehetősége egy gumimodell használata, melynek eredménye a kanyarmerevségek folyamatos változása lenne a dinamikai állapottól függően. A változó járműsebesség bevezetése a hosszirányú átterhelődést modellezné, mely a gumimodellel kombinálva jelentősen szélesítheti az értelmezési tartományt, elsősorban a gyorsabb irányváltások felé. A biciklimodell kétnyomú modellé való fejlesztése az oldalirányú átterhelődést is figyelembe venné, mely a gumimodellel, illetve a változó sebesség figyelembevételével feltehetőleg kielégítő lenne a mi járműirányítási igényeinknek.
Összefoglalás
Ideális kormányrendszer szabályozókörének fejlesztéséhez végeztünk előzetes vizsgálatokat. Lineáris jármű és SBW rendszermodellt állítottunk fel, melyek paramétereit identifikáltuk nemlineáris járműszimulátoron végzett mérések alapján. Az integrált rendszerre különböző szabályozókat terveztünk, melyeket a nemlineáris járműszimulátoron finomhangoltunk és a szabályozók performanciáit összehasonlítottuk. A lineáris modell értelmezési tartománya nagyon szűk, így megadtuk a modellfejlesztés további irányait, melyek már a nemlineáritás irányába mutatnak.
Köszönetnyilvánítás
A kutatást az ÚMFT TÁMOP-4.2.1/B-09/1/KMR-2010-0002 programja és az Országos Tudományos Kutatási Alapprogramok K-71762 projektje támogatta.
Irodalomjegyzék
[1] Zomotor Ádám: Gépjármű menetdinamika, IbB Mérnöki Szakértői Iroda, Budapest, 2006
[2] Lantos Béla: Irányítási rendszerek elmélete és tervezése I., Akadémiai kiadó, Budapest, 2005
[3] Lantos Béla: Irányítási rendszerek elmélete és tervezése II., Akadémiai kiadó, Budapest, 2003
[4] D.W. Gu - P.Hr. Petkov - M. M. Konstantinov: Robust Control Design with MATLAB, Springer, London , 2005
[5] Rödönyi G - Gáspár P : Robosztus szabályozó tervezése járműirányítási feladatok megoldására, A jövő járműve, II. évfolyam, 1-2. szám, 32-35.o, 2007
[6] Hankovszki Z – Kovács R – Palkovics L : Aktív kormánybeavatkozással kiegészített haszongépjármű-ESP, A jövő járműve, V. évfolyam, 1-2. szám, 57-63.o, 2010
[7] Control System Toolbox User’s Guide, MathWorks, 2010
[8] G Balas – R Chianf – A Packard – M Safonov : Robust Control Toolbox User’s Guide, MathWorks, 2010
[9] Y. E. Ko – C. K. Song : Vehicle Modeling with nonlinear tires for vehicle stability analysis, International Journal of Automotive Technology, Vol. 11, No. 3, pp. 339-344, 2010
[10] P Setlur – J R. Wagner – D M. Dawson – D Braganza : A trajectory tracking steer-by-wire control system for ground vehicles, IEEE Transactions on vehicular technology Vol. 55, No.1, pp. 76-85, 2006
[11] TESIS DYNAWare veDYNA 3.10 User Manual, Tehnische Simulation Dynamischer Systeme GmbH, 2010
[12] Bokor J - Gáspár P : Irányítástechnika járműdinamikai alkalmazásokkal, Typotex, Budapest, 2008
[13] Cs Fazekas : Models and Controllers of Steer-by-wire System, ThyssenKrupp Presta Report, 2010

Ajánló

Autótechnika
- A JÖVÕ MOBILITÁSA ELÕADÁSSOROZAT
- Suttogó fékbetétek: Akusztikai tesztek a fokozott fékezési
- VÁSÁRIDÕ
