ÖSSZEFOGLALÁS
A gyorsan fejlődő ipar és a gépesítés eredményeként jelentkező zaj többsége káros hatással van a környezetre és negatívan befolyásolja a komfortérzetet. Ennek következtében a szerkezetek akusztikai jellemzője jelentős hatást gyakorolhat azok piaci megítélésére és értékére. A tanulmány célja, egy pneumatikus rendszerben kialakult aeroakusztikus (aerodinamikai jelenségek által keltett) zaj numerikus áramlástani számítására alkalmas eljárás kidolgozása, illetve annak a mérési eredmények felhasználásával történő validálása. A módszer ciklikus alkalmazásával csökkenthető a fejlesztési költség, idő és kapacitás.

ABSTRACT
The noise, as an attending of the rapidly developing industry and product development can be harmful for human being and it has a negative effect for well-being. Thus, the acoustic characteristics of the engineering products can strongly influence their market demand. Hence, the goal of the present research is to develop a calculation procedure to simulate numerically aeroacoustic noise evolves in a complex pneumatic system and to validate the results by measurement. The cyclic application of the analyses can strongly contribute to decrease the development time, cost and capacity of a new product.

Bevezetés

Egy rendszernek fő feladata ellátásán kívül számos egyéb követelménynek is meg kell felelnie, amelyek csak másodlagosak, mégis jelentősen befolyásolhatják a rendszer kialakítását vagy éppen alkalmazhatóságát. Ilyen követelmény lehet a rendszer működése közben mérhető zajszínt adott érték alatt tartása, amely komoly kihívások elé állítja a mérnököket. Üzem közben jelentkező zaj ugyan nem okoz működési problémákat, azonban halláskárosodáshoz illetve vevői elégedetlenséghez vezethet. Emiatt ennek csökkentését megcélzó fejlesztési törekvések egyre nagyobb szerepet kapnak a teljes fejlesztési folyamatban.

Akusztikai szempontból a zaj és a hang ugyanannak a jelenségnek az eredménye, ami nem más, mint a légköri nyomás középérték körüli ingadozása. A rugalmas közeg nyomásváltozását kiváltó zavarás lehet egy vibráló felület (vibroakusztika) vagy az áramlásban létrejövő turbulencia is (aeroakusztika). Így a hang a rugalmas közeget érő gerjesztés hatására jelentkező, egymást követő kompressziós illetve expanziós hullámok következménye [2].

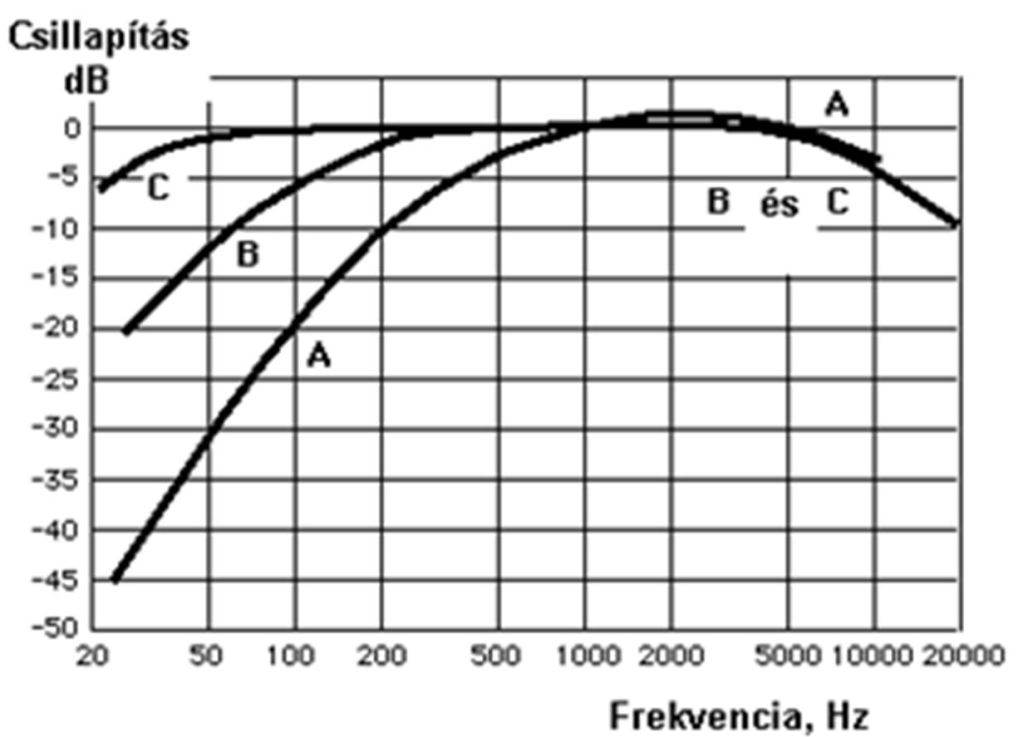
1. ábra: Különböző akusztikai szűrők csillapítási görbéi [1]

A tiszta hangokkal végzett vizsgálatok alapján kimutatható, hogy fülünk a mély és nagyon magas hangokra érzéketlenebb, a 3000 Hz körüliekre pedig érzékenyebb. Tehát bizonyos frekvenciájú hangokat az emberi fül csillapít, ennek mértékét az 1. ábra, az „A” akusztikai szűrő csillapítási görbéje szemlélteti. A szubjektív érzet frekvenciafüggősége arra késztette a műszergyártókat, hogy a mérőmikrofon és az objektív (dB) értékeket mérő műszer közé egy, a fül érzékenységét utánzó szűrőkört iktassanak. Ez valósítja meg az objektív mérőszámokkal leírható zaj és annak szubjektív hatása közötti kapcsolatot, amely nélkül az ember védelmére szolgáló elvárások, megengedhető értékek megállapítása lehetetlen lenne. A fentiek következményeként a szubjektív érzet figyelembevétele a zajcsillapítás és mérés szerves része kell legyen [1]. 

Az akusztikában igen széles értéktartományú mennyiségekkel számolunk. Hallásküszöbünk – az a legkisebb nyomás, amelyet még éppen meghallunk – 2*10-5 [Pa] körül van, míg az un. fájdalomküszöb kb. 20 [Pa]. Az érzékelt frekvenciatartomány alsó határa 20 [Hz] míg a felső 20 [kHz]. Ezen tartományok lineáris skálán való értelmezése nagyságuk miatt nehézkes, emiatt válik szükségessé a logaritmus skála bevezetése, amelyen a skála összezsugorodása miatt a hangnyomásszint (Sound Pressure Level - SPL) könnyen kezelhetővé válik. Ennek értéke, mint objektív mérőszám az alábbiak szerint számolható:

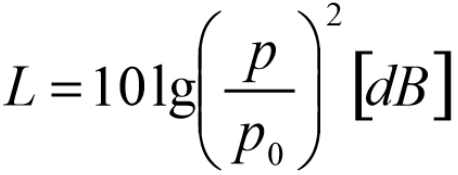
ahol a dB (decibel) a szintek mértékegysége. A referencia nyomás értékéül ( ) nemzetközi megegyezés alapján a hallásküszöböt választották, ami 2 x 10-5 [Pa] [3].

Az akusztikában nemcsak egyetlen tiszta un. „harmonikus”, időben szinusz, vagy koszinusz függvény szerint változó hang hatásával kell számolnunk. A legtöbb esetben az érzékelt hang több tiszta hang összetételéből áll. Bármilyen alakú is legyen a hangnyomás időbeli lefutása, mindig Fourier-sorba fejthető, azaz alkotóelemeire bontható. Ezzel meghatározható a zaj spektruma, ami a hangnyomásszint frekvencia függvényében való ábrázolása.

A ZAJ NUMERIKUS MODELLEZÉSE 

Zajcsökkentés szempontjából fontos a zajforrás és a zajtér ismerete, amihez a fentiek alapján a nyomástér, illetve annak időbeli megváltozása szükséges. A véges térfogatok elvén működő CFD (Computational Fluid Dynamics) szoftverek fontos részét képezik az akusztikai számításoknak, mivel alkalmasak az örvényekben, a turbulens áramlásban és a nyírórétegben kialakult nyomástér számítására is. Mivel ezek az áramlási szerkezetek hozzák létre a zavarást, az aeroakusztikai számítások során zajforrások is egyben. 

Az akusztikai szimulációk elvégzésére több lehetőség kínálkozik, amelyek közül a legpontosabb (jelen munkában használt) a CAA (Computational Aeroacoustics). Ennek során a teljes áramlási térre el kell végezni a tranziens számítást, melynek tartalmaznia kell a hangforrást, a megfigyelőt és a kettő közötti hangteret is [4]. Az eredmény megbízhatósága szempontjából lényeges a hangforráshoz közeli részek megfelelő mértékű időbeli és térbeli felbontása és számítása. Így pontosan meghatározhatók a zajforrások által keltett zavarások és azok terjedése a teljes áramlási téren keresztül az érzékelési pontig (megfigyelőig), ahol a statikus nyomás időbeli megváltozásának rögzítése történik [2]. Ez a megfigyelő által érzékelt nyomásjel (hangjel).

A legmagasabb frekvenciák kis tér- és időbeli felbontás, míg a legalacsonyabbak viszonylag hosszú szimulációs idő esetén lesznek elfogadható pontossággal kiértékelhetők. Az érzékelési pont gyakran többméteres távolságra van a zajforrástól. Emiatt az akusztikai számításnál a legtöbb esetben az áramlási tér mérete is nagyobb, mint a hangnyomásszint és a zajspektrum kiértékelését nem igénylő számítások esetében. A fentiek alapján kijelenthetjük, hogy a CAA szimulációk viszonylag nagyszámú időlépés és cellaszám mellett adnak pontos eredményt, ami megnövekedett számítási kapacitás igénnyel társul [2].

A nagyméretű örvények és turbulens struktúrák egyre kisebb méretűekre esnek szét, végül teljesen lecsillapodnak, mozgási energiájuk pedig hővé alakul át. Nyomáseloszlásuk és azok időbeli változásának számítása nem jelent problémát, azonban a numerikus hálóméreten aluli méretű struktúrák esetében ez már nem lehetséges. Hatásuk nem elhanyagolható, a turbulens áramlásnak ezt a részét turbulencia modellek segítségével vesszük figyelembe. A számítás során több turbulencia modellt vizsgáltunk meg, ezek összehasonlítására az eredmények kiértékelésekor kerül sor.

MÉRÉS ÉS ANNAK KIÉRTÉKELÉSE 

A pneumatikus egység (2. ábra) által kibocsátott zaj numerikus számításának validációja érdekében a hangnyomásszintet és a rendszer tömegáramát kell mérnünk. A tartályban lévő levegő nyomásának és hőmérsékletének ismeretében a valóságnak megfelelő peremfeltételeket tudunk beállítani a számításhoz, így ezek mérése is szükséges. Mivel a zaj ebben az esetben egy nagyon rövid tranziens folyamat (a levegő szűk keresztmetszeten nagy sebességgel történő átáramlásának) következménye, ezt a gyors változást a mérőműszerek nem képesek lekövetni. Ezért a mérés ideje alatt egy kvázi stacioner folyamatot kell biztosítani.

2. ábra: A vizsgált pneumatikus egység

A mérőberendezés két tartályt tartalmaz (3. ábra), ezek közül az A (27 [m3]) töltőtartályként, a B (0,5 [m3]) pedig puffer tartályként funkcionál. A levegő a tömegáramot mérő műszeren és egy 7 [mm]-es fojtáson áramlik át; innen a szelepbe, majd a környezetbe jut. A nyomás és hőmérséklet értékének mérése a B tartályban történik. A hangnyomásszint rögzítésére a rendszer kilépő keresztmetszete közelében előre kijelölt pontokban került sor.

 

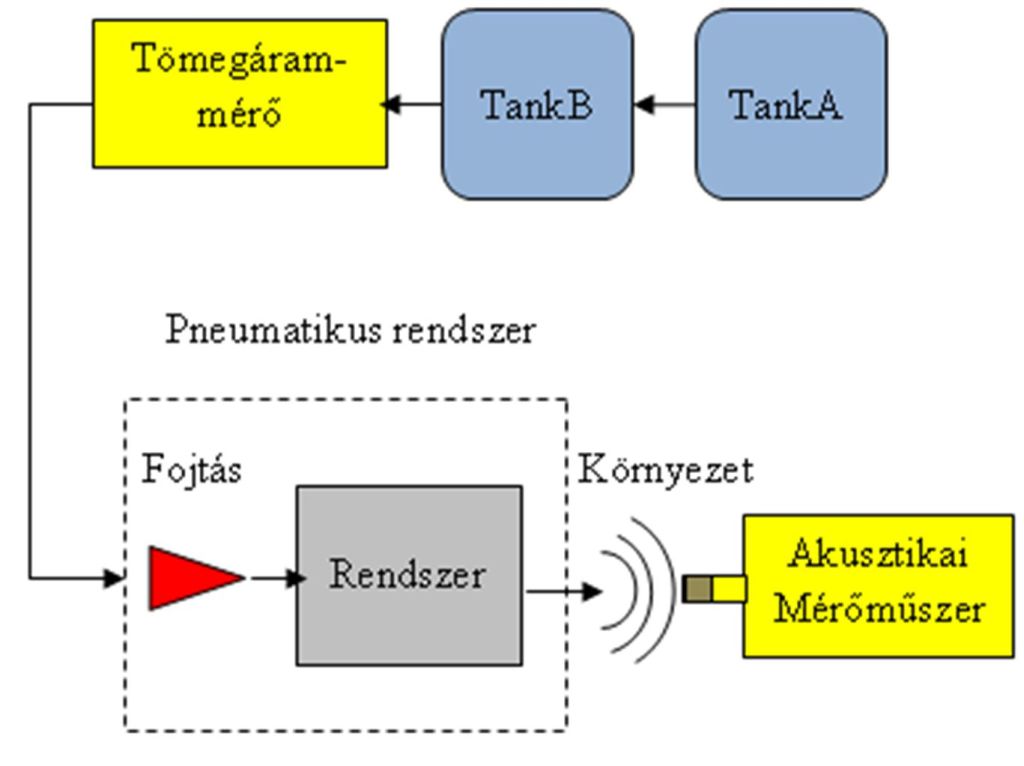
3. ábra: A pneumatikus rendszer felépítése

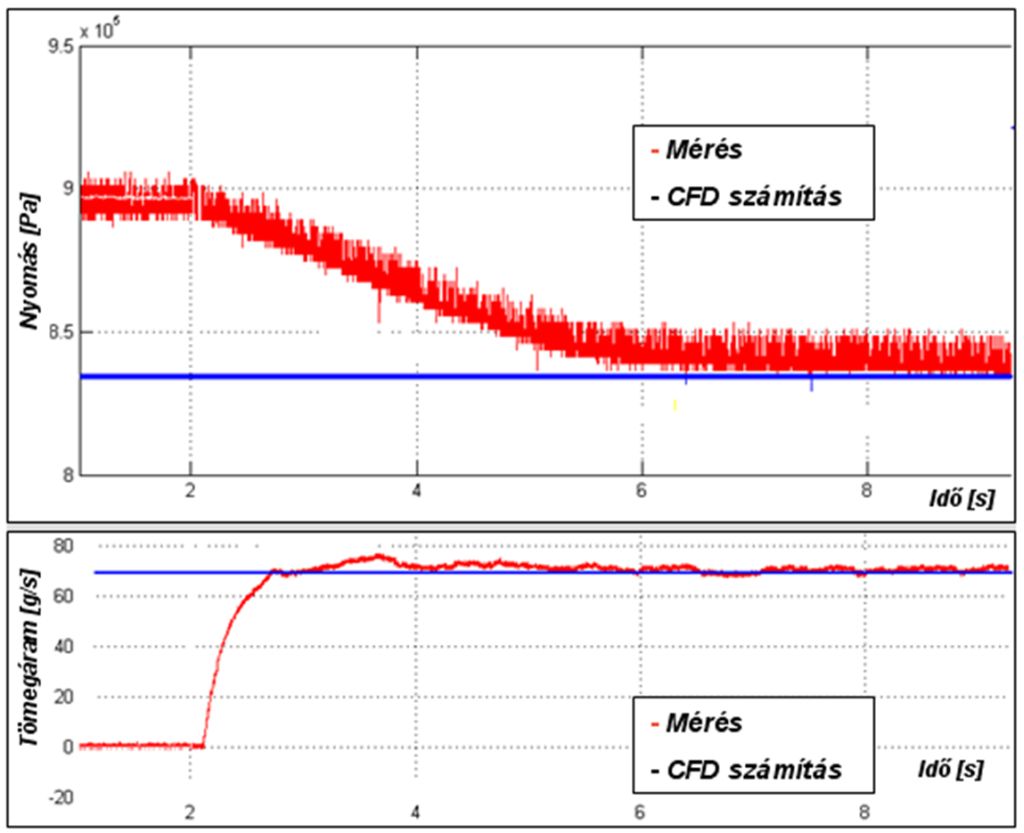
4. ábra: A nyomás és tömegáram mérésének eredményei

A mérés elején a B tartályban hirtelen leesik a nyomás, mivel az A tartály csak lassabban képes utántölteni (lásd 4. ábra fent). Ennek közel állandósult értéke kb. 8,4 [bar]. A mért tömegáram 70-75 [g/s], ez az érték jó egyezést mutat a program által végzett számítás során kapott 70 [g/s] értékkel (lásd 4. ábra lent).

Az 5. ábra egy mérési pont „A” akusztikai szűrő szerinti zajspektrumát szemlélteti, amelyhez hasonló karakterisztikájú spektrumot kapunk a többi mérési pontban is. A mérések 3 [s]-ig tartottak és az állandósult nyomásértékhez tartozó időtartományban lettek végrehajtva (4. ábra). Látható, hogy a zaj kialakulásában a magasabb frekvenciákhoz tartozó komponensek dominálnak, ennek eredménye egy magas éles hang. A bemutatott zajspektrumhoz 128,8 [dB] „A” súlyozásos hangnyomásszint tartozik, amihez képest a háttér zaj hangnyomásszintje elhanyagolható, tehát korrekcióra nincs szükség.

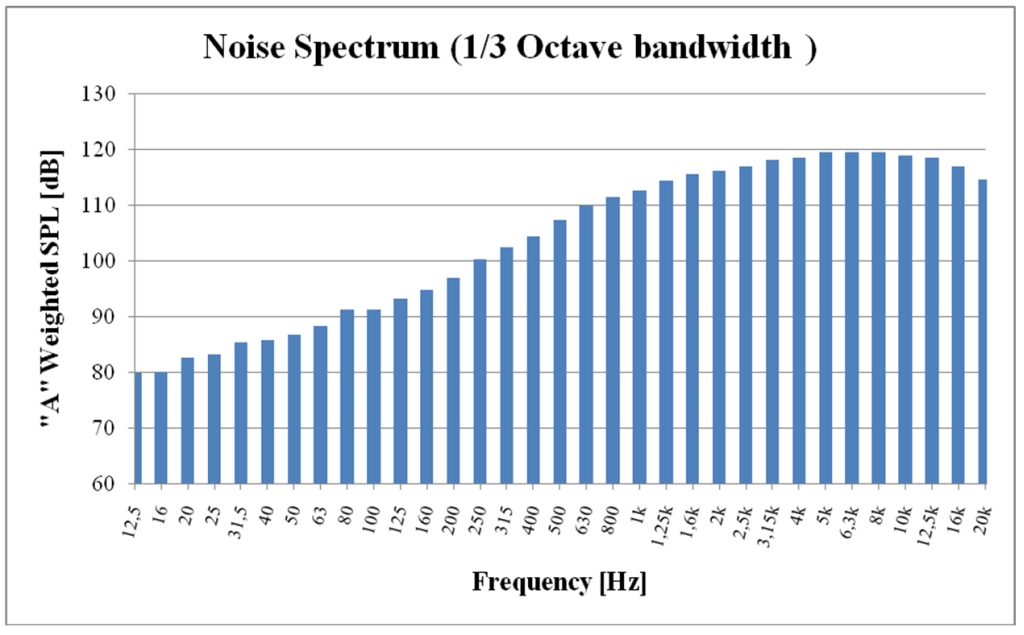
5. ábra: Zajspektrum egy mérési pontban

NUMERIKUS SZIMULÁCIÓ ELŐKÉSZÍTÉSE

Első lépés az áramlási tér elkészítése volt a geometria alapján. A 6. ábra jobb oldalán láthatjuk a vizsgált egység áramlási terét, amelyhez a mérésnek megfelelően egy 3 [m] hosszúságú cső csatlakozik (lásd 7. ábra). Ennek másik végén helyezkedik el a B tartály, melyet a végső áramlási tér nem tartalmaz, hatását a cső végére, mint a rendszer bemenetére definiált állandó 8,5 [bar] nyomással vettük figyelembe. 

6. ábra: A vizsgált egység és áramlási tere

A zajszintet a mérés során természetesen a pneumatikus rendszeren kívüli pontokban tudtuk csak meghatározni, így a szimuláció során is ugyanott kell elhelyeznünk az érzékelési pontokat. A környezet figyelembevételére a teljes áramlási teret egy téglatesttel határoltuk körbe (lásd 7. ábra). A téglatest oldallapjai súrlódásos adiabatikus kimenet nélküli falként kerültek definiálásra, mert a kimenettel rendelkező nagy áramlási tér a kilépésre érzékeny CFD megoldó esetében konvergencia problémákhoz vezetett volna. A pneumatikus egység és a hozzá csatlakozó cső felületei szintén fali (no-slip) peremfeltételként lettek megadva.

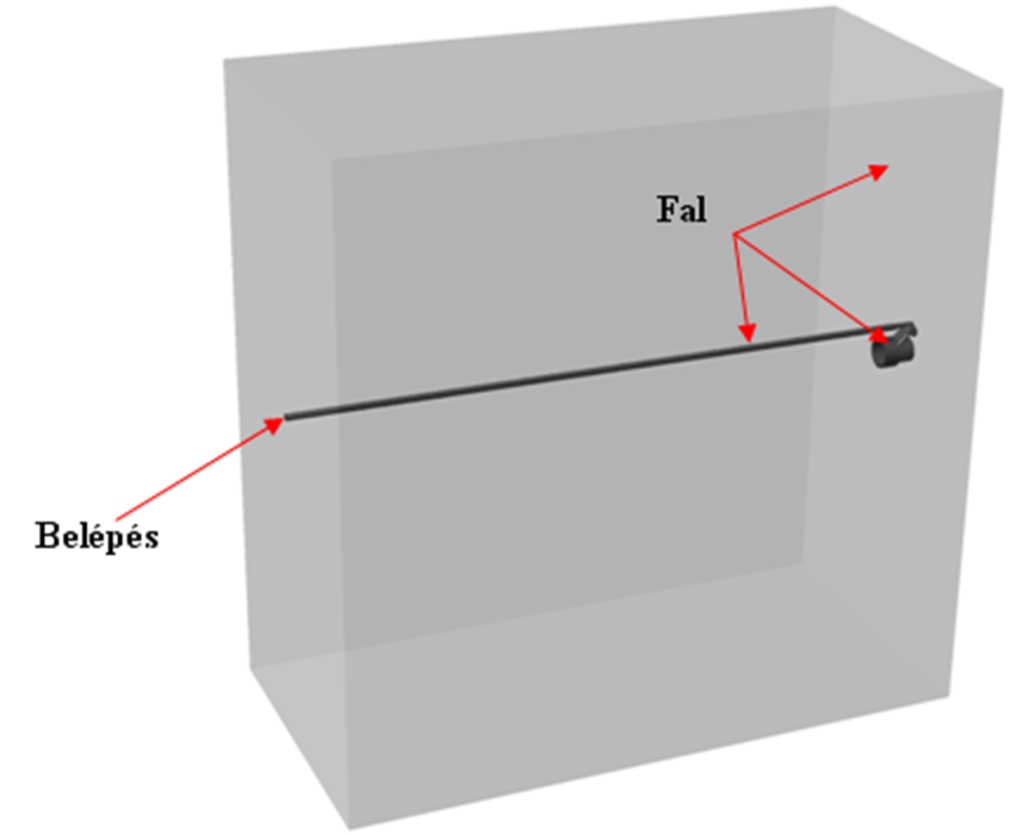
7. ábra: A rendszer peremfeltételei 

Mivel a szimuláció során hangnyomásszintet is szeretnénk számolni, fontos a turbulencia pontos modellezése. Ezért a szimuláció során több turbulencia modellt is alkalmaztunk, így lehetőségünk nyílik ezek összehasonlítására a kiértékelés során. Az alkalmazott modellek a következők: Shear Stress Transport (SST), Scale Adaptive Simulation (SAS) és Detached Eddy Simulation (DES).

NUMERIKUS SZIMULÁCIÓ EREDMÉNYEI

Az egységbe való belépésnél a mért nyomás értéke 8,34 és 8,4 [bar], a tömegáram pedig 70 és 75 [g/s] között volt (lásd 4. ábra). Ugyanezek az értékek a CFD számítás eredményei alapján 8,34 [bar] és 70 [g/s] (lásd 4. és 8. ábrák). Megállapíthatjuk, hogy a számítás és a mért eredmények jól korrelálnak egymással, így a nyomás és tömegáram validációját elfogadhatjuk.

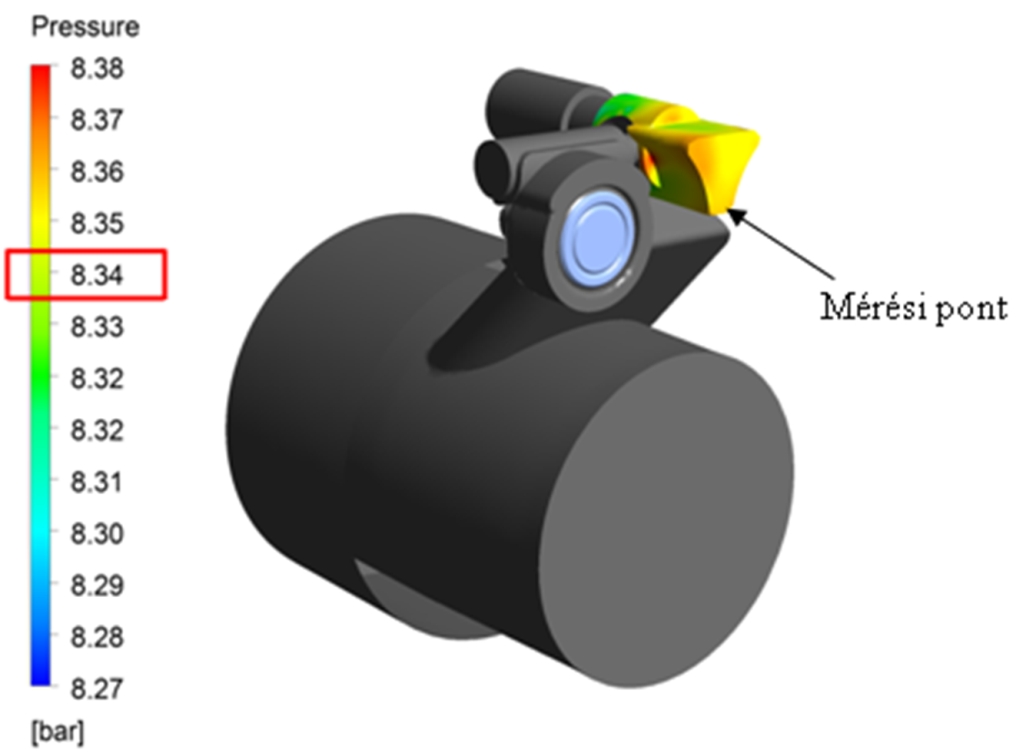
8. ábra: Számított nyomásérték a mérési pontban

A 9. ábrát megfigyelve azt a további következtetést vonhatjuk le, hogy mindegyik turbulencia modell visszaadta a mérési eredményt 3 és 5 [kHz] közötti frekvenciatartományban elfogadható hibahatáron belül. Ez az emberi fül számára a legérzékenyebb tartomány, ami az „A” akusztikai szűrő  karakterisztikájából is kiderül (lásd 1. ábra). Érdemes megemlíteni, hogy a szakirodalomban fellelhető adatokkal ellentétben az SAS turbulencia modell pontosabb eredményt adott, mint a DES.

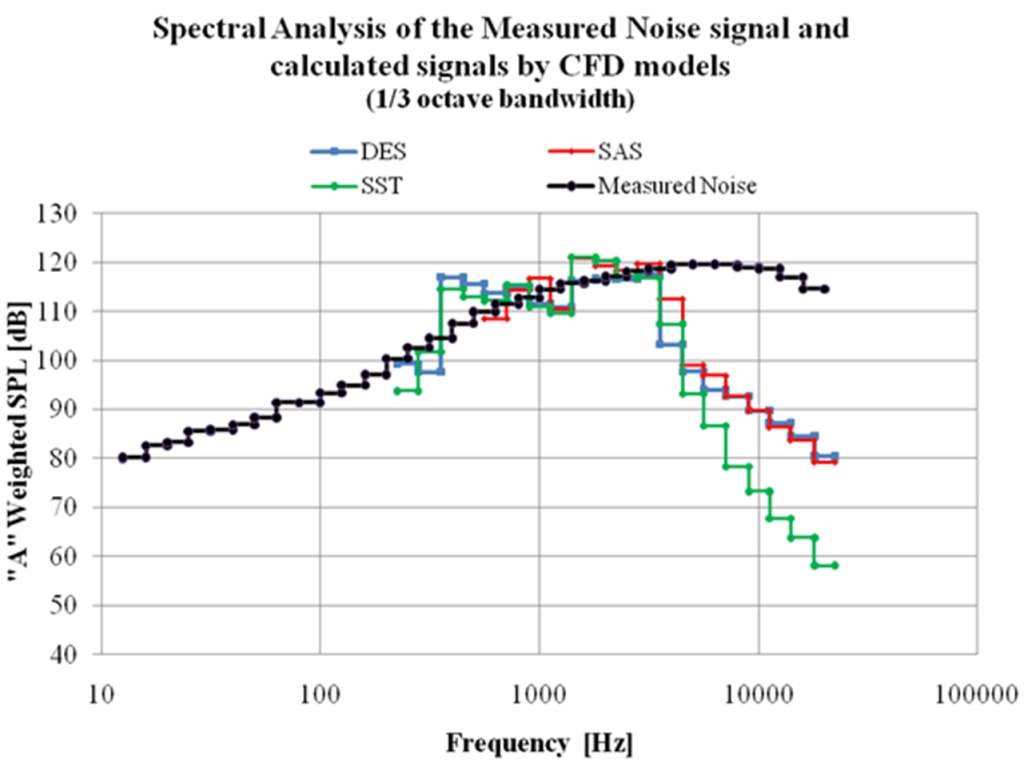
9. ábra: A mért és számított zaj spektruma

A nem elegendően diszkretizált áramlási tér, illetve turbulencia modellek csillapító hatása miatt kevésbé pontosak a magasabb frekvenciatartományokon, ezért itt viszonylag nagy eltérés tapasztalható a mért és számított spektrumok között. 

A legmagasabb kiértékelhető frekvenciát (fmax) az időlépés (deltat) határozza meg a következő összefüggés szerint:

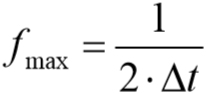
Az időlépés esetünkben 10^-5 [s], volt így a frekvencia maximális értéke 50 [kHz], ami a hallható tartományon kívül esik. A frekvenciatartomány alsó értékének számításához a szimulációs időtartam (tflow) és a legalacsonyabb frekvencia (fmin) közötti kapcsolatot használhatjuk fel:

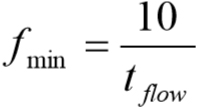
Mivel a szimulációs időtartam 0,02 [s] volt, így a megoldó által számolt legkisebb frekvencia 500 [Hz]. Ha a teljes tartományt le szeretnénk fedni 20 [Hz]-től kezdve, akkor 0,5 [s] időtartományt kellett volna a teljes folyamatból kiszámolni, ami lényegesen hosszabb számítási időt eredményezett volna. Így, az 500 Hz kompromisszum alapján lett kiválasztva, az ez alatti frekvenciatartományt nem tudjuk figyelembe venni. 

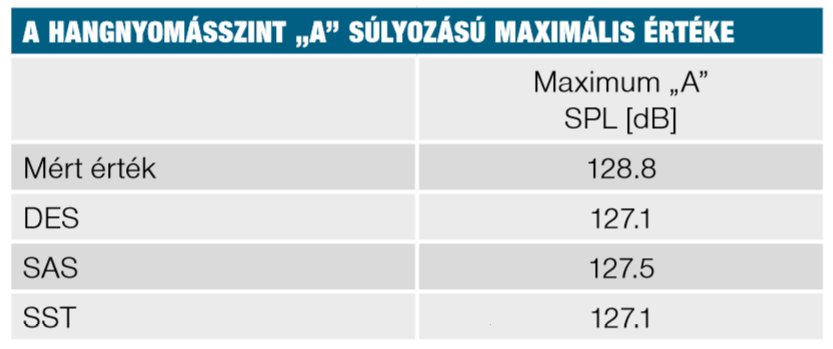
1. Táblázat: Turbulencia modellek eredményeinek összehasonlítása.

Az 1. Táblázat egy kiválasztott mérési pont „A” akusztikai szűrő súlyozásával kapott hangnyomásszint maximális értékét adja meg. A számítások eredményei kevesebb, mint 2 [dB]-el térnek el a mérési eredménytől. Összevetve a hangnyomásszint értékét és a zajspektrum képét megállapíthatjuk, hogy a legpontosabb eredményt az SAS turbulencia modell adta, a legrosszabbat pedig az SST. 

ÖSSZEFOGLALÁS

A tanulmány célja egy pneumatikus rendszer által keltett aeroakusztikus zaj numerikus áramlástani modellezése CFD szimuláció segítségével elfogadható számítógép kapacitásigény mellett. A zaj kiértékelése során a hangnyomásszint, illetve a zajspektrum meghatározására került sor előre definiált pontokban. A vizsgált pneumatikus egységen végzett mérés eredményei egyrészt a numerikus szimuláció bemenő paramétereinek meghatározására, másrészt a számítás validálására szolgáltak. A szimuláció során több turbulencia modell került alkalmazásra. A mért és számított eredmények összevetése alapján kijelenthetjük, hogy a szimuláció a valóságnak megfelelő értéket adott a nyomás és a tömegáram értékére vonatkozóan. A zajspektrum esetében az emberi fül számára legérzékenyebb tartományban (3 - 5 [kHz]) a számítás visszaadta a mérési eredményeket. A turbulencia modellek összehasonlítása során a megvizsgált három modell közül az SAS modell bizonyult a legpontosabbnak.

KÖSZÖNETNYILVÁNÍTÁS

A munka szakmai tartalma kapcsolódik a "Új tehetséggondozó programok és kutatások a Műegyetem tudományos műhelyeiben" c. projekt szakmai célkitűzéseinek megvalósításához. A projekt megvalósítását a TÁMOP-4.2.2.B-10/1--2010-0009 program támogatja.

IRODALOM

• Dr. Kurutz Imre, Dr. Szentmártony Tibor – A műszaki akusztika alapjai, 1991

• Domenico Caridi – Industrial CFD simulation of Aerodynamic noise (http://www.fedoa.unina.it/3249/2/ Tesi_Dottorato_Caridi-2008.pdf), 2008

• Lajos Tamás – Az áramlástan alapjai, 2008

• ANSYS CFX 12.1 documentation