Autóbusz futóművének dinamikai modellezése

ÖSSZEFOGLALÁS

Ezen cikk egy autóbusz dinamikai viselkedésével foglalkozik, annak síkbeli szimulációs modelljén keresztül. A szimuláció elsődleges célja a futóművekre ható terhelések vizsgálata, illetve a szimulációval való nyomon követésük létjogosultságának eldöntése. A modell épp ezért nem csak a jármű hossz-, és függőleges irányú mozgásait képes kezelni, de a futóművek járműtesthez viszonyított hosszirányú mozgását is. A szimuláció validálását a RÁBA Futómű Fejlesztési Intézet által a közelmúltban elvégzett többhetes mérés tette lehetővé. Ennek során a BKV Zrt. Ikarus 435T buszán végeztek futómű terhelésvizsgálatot. 

ABSTRACT

The article deals with the dynamic behavior of a solo and an articulated vehicle through a two-dimensional simulation model. The primary objectives of the simulation are studying the loads acting to the suspensions, and the legitimacy of tracking with simulation to decide. Therefore the model is not only able to track the vehicle longitudinal, and vertical movements, but the axle longitudinal movement relative to the vehicle body is handled as well. The validation of the simulation is made possible by the measurements carried out by the RABA Chassis Development Institute, where a BKV Ikarus 435T bus was tested.

 

Bevezetés

A tervezési folyamat során az egyik legnagyobb figyelmet igénylő munka a dinamikus terhelésre igénybe vett alkatrészek méretének meghatározása, és azok élettartam-szilárdságra történő méretezése, illetve ellenőrzése. Az ellenőrzéshez legkézenfekvőbb az adott alkatrész üzemszerű terhelés közbeni mérése, terhelésvizsgálata.

Számos területen azonban nem mindig lehetséges a mérést egyszerűen kivitelezni, illtetve nem minden jellemző mérhető. Ilyen például a futóművek terhelésének felvétele, amihez bonyolult mérőrendszer, több hetes előkészületi és felszerelési idő kell, továbbá jármű sem áll mindig rendelkezésre. Egy jármű futómű teljes terhelésének felvételével azonban jó alapot kaphatunk a kifáradásra történő méretezéshez. Egy ilyen terhelés lefutásának megfelelő kiértékelése alkalmas bemenetként szolgálhat a különböző szilárdsági végeselemes alkalmazások megoldóinak.

A mérési kényszer kiküszöbölésére kezdtük el fejleszti az alább bemutatott járműmodellt. Ennek megfelelő felépítése és validációja lehetőséget kínál a további futómű vizsgálatokhoz és tervezéshez, mivel előre jelezhetőek bizonyos nehezen mérhető igénybevételek. Egy megfelelő pontosságú modell mind jelentős anyagi, mind időbeni megtakarítást jelent.

A későbbi, pontos szimulációkhoz természetesen ismernünk kell – bizonyos pontossággal – az üzemi viszonyokat. Közösségi járművek esetében ilyen üzemi viszonyok pl.: a bejárt vonal menti utasterhelés eloszlás; megállók, kötelező piros lámpák közötti távolság, illetve az útprofil minősége. Ezek ismerete nélkül a modell csak az út emelkedéséből, illetve lassulás és gyorsításkor bekövetkező átterhelődésekből képes számolni. Az útgerjesztés, a keresztirányú mozgás kezelése, alternatív hajtáslánc vizsgálatára is alkalmas eszközök implementálása további kutatást igényel. Távlati terveink között szerepel ugyanis különböző járműhajtási módok modell alapú vizsgálata is. A modell ezzel együtt alkot majd egy komplex járműdinamikai vizsgálatokra alkalmas eszközt.

A továbbiakban szemléltetett modell validációját az útprofil ismerete nélkül végeztük, ezért a futóműre ható függőleges erőhatások a várttól némileg eltérnek. A modell síkbeli, tehát az erőhatásokat az egyes irányok menti eredőként tudja kezelni. A fejlesztés további fázisaiban alkalmassá tesszük a jármű keresztirányú-, illetve a futómű egyéb parazita mozgásainak figyelembe vételére is. A modellt MATLAB/Simulink környezetben került implementálásra. 

 

Jármű bemutatás

A modell alapjául szolgáló jármű egy a BKV Zrt. tulajdonában lévő Ikarus 435T trolibusz, mely a 304-es vonalon fut. Magaspadlós, középmotoros, B tengelyén hajtott kivitel. A jármű fontosabb műszaki adatait az 1. táblázat tartalmazza: 

A járműves mérés során rögzítésre kerültek: a jármű mindenkori koordinátái (megtett út), aktuális tengerszint feletti magasság, kardántengely nyomaték, kardántengely fordulatszám, oldalankénti kerékfordulatszám, légrugó nyomások és a futómű kikötőrudaiban ébredő erők a mért hídon. Logikai jelként rögzítésre kerültek továbbá azok az időintervallumok, melyekben a járművezető az egyes fékeket használja. Ebből kiderül, hogy szinte a teljes lassulás fázisában csak a villamos fék aktív, míg a mechanikus fékműködtetés kb. 5 km/h sebességnél lép életbe. A mechanikus fék működéséről azonban nem állt rendelkezésre rögzített információ, ezért a validáció során az 5 km/h sebesség alá való lassítási szakaszokat nem használtuk.

 

Futómű bemutatása

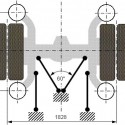
Az IK435T buszok B tengelye a ZF AV-131/90 típusjelzésű futómű. A hajtáshoz szükséges 11,26-os áttételt két fokozat valósítja meg. A kúpkerék-differenciálmű tányérkerék áttétele 3,529, míg az oldalhajtásé 3.19. Az oldalhajtásban oldalanként két szabadonfutó fogaskerékkel tették lehetővé a differenciálmű tengelyének a kerekek forgástengelyétől való lesüllyesztését, ezzel az alacsonyabb hasmagasság kialakíthatóságát. A futómű fontosabb adatait a 2. táblázat tartalmazza: 

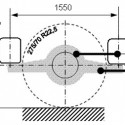
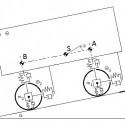
 A futómű beépítési környezete és egyszerűsített rajza az 1. ábrán látható: 

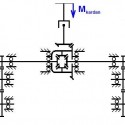
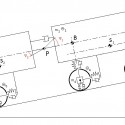
 A szimulációban a tengelyhez kapcsolódó hatáslánc és a karosszériáról és úttest gerjesztéseiből átadódó külső terhelések kerültek modellezésre. A híd külső terheléseit a hajtó nyomaték, a kikötőrudak, illetve légrugó nyomásból számítható erők jelentik. Az egyes kikötőrudakban ébredő erőt nyúlásmérő bélyeggel mérték, míg a légrugóerőt első közelítésben annak statikus karakterisztikájának segítségével számíthatjuk a nyomásokból. A hajtásláncot terhelő nyomaték mérése kizárólag a kardántengelybe épített nyomatékérzékelővel volt lehetséges, a bemenő fordulatszám viszont a differenciálmű kúpfogaskerekének fordulatszáma. Mindezt azért lényeges leszögeznünk, mert a vételi pont között található egy kardáncsukló, melynek torzító hatása közismert. Tény viszont, hogy az adott járműben a beépítési környezet olyan, hogy a kardántengely közel párhuzamos a differenciálmű behajtó tengelyével. A kardáncsukló torzító hatásának figyelembe vételéhez azonban ismernünk kellene a futómű mindenkori helyzetét a karosszériához viszonyítva. Egy csukló szögsebességátvitelének pontos összefüggését bonyolult trigonometrikus függvény írja le, mely a szimulációs modellben további nemlinearitást jelentene. Ezzel jelentősen összetettebbé válna a modell. A fenti okok miatt úgy vesszük, minta a bemenő nyomatékot és fordulatszámot azonosan a kúpkeréken mértük volna. A híd hajtásláncát a 2. ábra szemlélteti egyszerűsített formában: 

 

Szimulációs modell

A teljes modell két alrendszerből áll. Az egyik a jármű menetdinamikai folyamatait kezeli, a másik a hajtásláncot modellezi. A szimuláció fejlesztése során párhuzamosan került sor egy szóló és egy csuklós autóbusznak megfelelő modell kiépítésére. Így azonos bemenő adatok esetén mérlegelhetővé válik a két modell közötti különbség a futómű terhelések szempontjából. Ez annyit jelent, hogy egy ugyancsak létező, szóló jármű paramétereit felhasználva, a csuklós járműével megegyező tömegű buszban is megvizsgálhatjuk a futóművet.

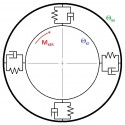
A szóló busz általánosított járműdinamikai modelljét a 3. ábra, míg a csuklós busz modelljét a 4. ábra szemlélteti. A szóló jármű részletes modelljében találunk egy haladó-forgó tömeget (karosszéria), két haladó (futóművek) és két forgó mozgást végző tömeget (kerekek, és a nem hajtott forgó egységek tehetetlensége a futóműben). A mérlegelési térfogatok száma tehát: öt [1]. A teljes modell szabadságfoka 9. A modell egyes szabadságfokok szerinti mozgásegyenleteit célszerűen a súlypontra írjuk fel. 

 A csuklós busz modellje a szólóhoz képest kiegészült egy további karosszéria és egy futómű egységgel. Mivel a két karosszériaelem között idealizált merev csuklós kapcsolat van, ezért a két elem hossz- és függőleges irányú mozgása csatolódik. Ezért a rendszer szabadságfokainak száma: 

Ebben az esetben a mozgásegyenleteket a csuklópontra célszerű felírni, mert így nem maradnak ismeretlen erők az egyenletben. A két karosszériaelem között egy további csillapító került definiálásra. Eredendően ez a csillapító a keresztirányú kígyózást hivatott csökkenteni, azonban a csuklóponttól vett függőleges távolsága miatt a két karosszériaelem bólintását is csillapítja. 

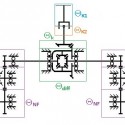
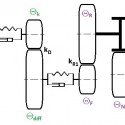
Mindkét járműmodellben azonos elem a hajtáslánc [2]. Ennek dinamikai modelljét a 2. ábra alapján állíthatjuk össze. Egyes forgó tömegek között lineáris torziós rugót és csillapítást, mások között merev áttételt feltételezünk. Utóbbiak a hajtás hatásfokának és módosításának figyelembevételével összevonhatók. A dinamikai modellben szereplő tömegek elkülönítését az 5. ábra szemlélteti, az előbb jelzett összevonhatóságot az azonos szín jelzi. 

A hajtáslánc utolsó elemének, a keréknek dinamikai modelljét a 6. ábra ismerteti. A keréktárcsa és gumiabroncs között rugalmas sugárirányú és torziós kapcsolatot tételezünk fel. 

A kerékmodellben a vastag körgyűrű jelenti a gumiabroncs kerületre redukált tehetetlenségét, a keréktárcsa pedig (θKT) a továbbiakban a kerékagy tehetetlenségével kerül összevonásra. A keréktárcsa tehetetlensége ily módon a hajtáslánc, míg a gumiabroncs tehetetlensége a járműmodell paramétere lesz. A két alrendszer közötti csatolást a hajtáslánctól a járműmodell irányába a keréknyomaték, míg ellentétes irányban a gumiabroncs fordulatszáma végzi.

A két részmodell összevonva képezi a teljes hajtáslánc dinamikai modelljét (7. ábra). A pontos modell érdekében figyelembe vettük az egyes csapágyak súrlódó nyomatékát és a fogaskerék áttételek hatásfokát. 

Az egyes tehetetlenségek:

θK1:                 kardántengely és fél kardáncsukló
θK2:                 fél kardáncsukló és fél kúpkerék
θk:                   fél kúpkerék
θdiff:                 differenciálmű és féltengely
θF:                   féltengely és a két behajtó fogaskerék
θR:                   áthajtó fogaskerekek az oldalhajtóműben
θNF:                 kétoldali kihajtó fogaskerék
θA:                   kerékagyak, fékdobok, keréktárcsák
θGK:                 gumiabroncsok tehetetlensége
kD:                   differenciálmű módosítása
kR1:                  oldalhajtás első fokozatának módosítása
kR2:                  oldalhajtás második fokozatának módosítása

A szimuláció során a járművet v0 kezdősebességgel indítjuk. A karosszéria helyzete olyan, mintha az egész járművet felemeltük volna egy h0 kezdeti magasságra, ahol a futómű rugói és a gumiabroncsok is tehermentesülnek, de a kerekek még épp érintkeznek a talajjal. Erre azért van szükség, hogy a továbbiakban kezelni tudjuk a gravitációs erőtér hatását. A szimuláció első pár másodpercét tehát arra szánjuk, hogy beálljon a valóságnak megfelelő leterhelt helyzetbe. 

Mindazért, hogy a karosszéria függőleges irányú lengései ne befolyásolják a lényegi szimulációt, a lengés lecsillapodásáig hagyjuk szabadon futni a járművet. A 8. ábrán látható a bemenő nyomaték mint modellbemenet és a kúpkerék fordulatszáma. Ennek során kellően változik a modell gerjesztése ahhoz, hogy értékelni tudjuk a rendszer viselkedését. A jármű sebessége a fordulatszámhoz hasonló lefutású, azzal közelítőleg arányos jelként képezhető.

A gumiabroncs és az útfelület közötti erőkapcsolati tényező modellezésére a Hans B. Pacejka által kidolgozott formulát használtuk [3].

A modell legtöbb paramétere pontosan ismert fizikai vagy geometriai mennyiség. Azonban számos olyan adat van, melynek értékére nincs szakirodalmi utalás, vagy nincs róla mérési eredmény. Ezért a modellépítés során a következő egyszerűsítéseket feltételeztük:

1.  A gumiabroncs radiális merevségét az elmozdulással arányosnak vesszük. Némi elméleti megfontolással a merevségi karakterisztikának két jól behatárolható pontja van: az egyik a kirugózott állapotot jelöli, ahol a gumiabroncs nem visz át radiális irányú erőt. A másik helyzet a defektnek megfelelő, mikor a gumi felütközik a keréktárcsán. Ilyenkor kvázi végtelen nagyságú erőt közvetít. A gumiabroncs merevsége az elmozdulás függvényében tehát progresszív, annak pontos meghatározására további mérések szükségesek.

2. A kikötőrudak esetében szintén egyszerűsítéssel éltünk. Azokat általánosan rugalmas, lineáris karakterisztikával látjuk el, ám valós jellegük sokkal inkább hasonlít egy gumibak és hozzá kapcsolt merev fémrúd karakterisztikájának szuperpozíciójához.

3.  Leginkább ismeretlen tényező a légrugó, és az előbb említett gumiabroncs és kikötőrúd csillapítások. Ezek mindegyikét lineárisnak feltételezzük.

4.   A szimulációnak nem képezte bemenetét az út egyenetlenségeiből adódó gerjesztés.

5.  A valós jármű mindenkori függőleges helyzetét szintszabályzó felügyeli. Ennek hatását a modell nem veszette figyelembe.

 

Szimulációs eredmények és Modell validáció

A két modell eredményeinek elemzésekor kiderült, hogy azok nagyon hasonlóan viselkednek adott bemenetre. Ezért a szóló és csuklós busz szimulációs eredményeinek értékelésekor az áttekinthetőség végett csak a szóló busz eredményeit mutatjuk be.

A 9. ábra egy tíz másodperc időtartam alatt lejátszódó gyorsítási szakaszt szemléltet. Összehasonlítva a mért és szimulált kúpkerék fordulatszámokat látható, hogy a modell jó egyezést mutat.

A 10. ábrán a légrugók nyomásából adódó erő látható. A kezdeti tranziens a fent leírt nyugalmi helyzet megtalálása előtti időtartam. Az eredő légrugó erő a mértnek megfelelő középértékre áll be, azonban a dinamikus terhelésváltozásokat az előbb említett gerjesztések hiányában nem képes követni. Jól látszik, hogy a 4-től 9 másodpercig tartó aktív gyorsítási szakaszban az átterhelődésnek köszönhetően csekély mértékben megnő a rugóerő. 

A 11. ábra a kikötőrúderőket hasonlítja össze. Elmondhatjuk, hogy a modell jellegre és mértékileg is követi a mérést. Bizonyos pontokban azonban jól látszik az útgerjesztés hiánya. 

Valamivel a 7. másodperc előtt kisebb jellegbeli eltérés mutatkozik, ami azzal magyarázható, hogy a kerék felfutott egy úthibára, ami a kikötőrudak terhelését egy pillanatra csökkentette. Nehezebbnek tűnik értékelni a kezdeti nyomatéklépcső szakaszát. Ha összehasonlítjuk a 9. és 11. ábrákat látható, hogy a szimulációban a kikötőrudakban ébredő erő az elvárásoknak megfelelően viselkedik. Növekvő nyomatékra növekvő rúderővel válaszol. A méréssel történő összevetés azonban jelentős különbséget mutat. Itt feltételezhető, hogy a kerék egy mélyedésben állt indulásnál, aminek leküzdése produkálta az ábra szerinti terheléslefutást. Ez megmagyarázná a kezdeti fordulatszám eltérését is.

 

Következtetések és kitekintés

Általánosan elmondható, hogy a modell járműdinamika része jellegre jól követi a méréseket. A fordulatszám görbék meredeksége között tapasztalható némi eltérés. A későbbiekben alkalmassá tehető különböző hajtáslánc típusok közötti különbségek vizsgálatára. Külön a hajtáslánc viselkedésére nincs ellenőrzési lehetőség, de annak jelenlegi pontossága megfelelő a járműmodell viselkedésének értékeléséhez. A modell még koránt sem mondható véglegesnek, jelentős fejlesztések rejlenek benne. Mindenekelőtt a fentebb leírt közelítések helyett egzakt jelleggörbék alkamazásával javítható a modell valósághűsége. Az útprofil pontos felvétele és gerjesztő hatása a járműkerékre máig nem megoldott probléma. Ennek pontos kikutatásával jelentősen nőne az ehhez hasonló modellek értéke. További kiegészítés tehető a hajtásláncban az alkatrészek közötti hézag modellbe építésével. Ennek jelenléte ugyan nemlinearitást okoz, de a teljesség igényéhez hozzá tartozik.

Azt kell mondjuk, hogy a kikötőrudakra vonatkozó szimulációs rész még a fent leírt durva egyszerűsítésekkel együtt is elvárásokon felül közelíti a valóságot. Ezzel együtt elmondható, hogy bár nem a szóló jármű kikötőrúd terhelései kerültek mérésre, a modell finomításával alkalmasnak mondható különböző busztípusok futómű terheléseinek megítélésére. A téma ezek szerint helytálló kutatási terület és igazi kiaknázatlan kincsesbánya, mert pontosításához további területek kutatása, és mérések sokasága szükséges.

 

Köszönetnyilvánítás

Köszönet illeti a RÁBA Futómű Fejlesztési Intézet munkatársait a készséges támogatásért, mellyel munkámat segítették. A jármű hajtáslánc modellje nem jöhetett volna létre a Protruck Kft. szakemberei nélkül, akik idejüket nem sajnálva álltak rendelkezésünkre, ezzel hozzájárulva a cikk megírásához. Köszönetünket fejezzük ki érte!

Irodalom

• K. M. Hangos, I. t. Cameron: Process Modelling and Model Analysis, Academic press (2001).
• trencséni, B., németh, H. Integrated powertrain modelling to enhance comfort of heavy duty vehicles, Proceedings of the 22nd JUMv science and Motor vehicles Conference (2009).
• Hans B. Pacejka: tyre and vehicle Dynamics, Butterworth-Heinemann ltd; 2nd Revised edition edition (8 Dec 2005).

 

 

Ajánló

Autótechnika

• A JÖVÕ MOBILITÁSA ELÕADÁSSOROZAT
• Suttogó fékbetétek: Akusztikai tesztek a fokozott fékezési
• VÁSÁRIDÕ

Szakkönyvek